Problem 524: Circle, Equilateral Triangles, Midpoint, Side, Measurement. Level: High School, SAT Prep, College geometry

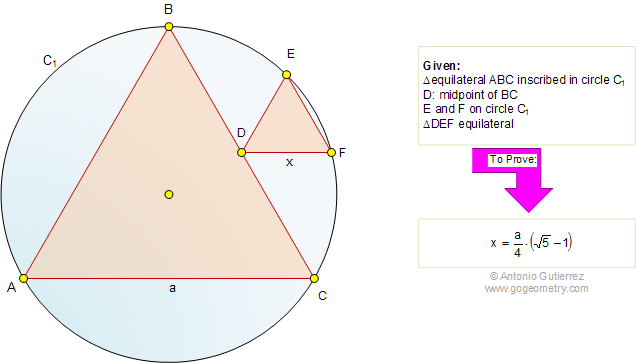
The figure shows an equilateral triangle ABC (side a) inscribed in a circle C₁. The point D is the midpoint of BC and E and F are on the circle C₁. If the triangle DEF is equilateral (side x), prove that 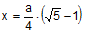. Post a comment or solution.
 

Reference: Fukagawa Hidetoshi, Tony Rothman, "Sacred Mathematics: Japanese Temple Geometry" (Princenton University Press, 2008).

See also:

Problem 525.
Circles, Diameter, Tangent, Radius, Congruence, Measurement.

Problem 523.
Tangent Circles, Diameter Perpendicular, Collinearity.

Problem 522.
Right Triangle, Circle, Diameter, Tangent.