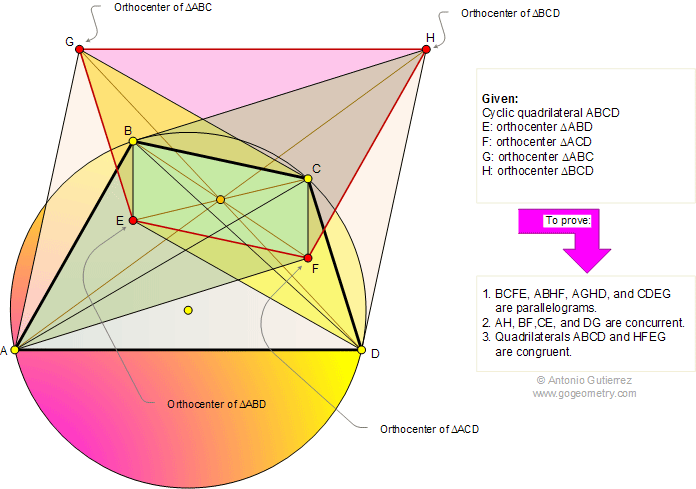
The figure shows a cyclic quadrilateral ABCD. The points E, F, G, and H are the orthocenters of triangles ABD, ACD, ABC, and BCD, respectively. Prove that (1) BCFE, ABHF, AGHD, and CDEG are parallelograms, (2) Lines AH, BF, CE, and DG are concurrent, (3) Quadrilaterals ABCD and HFEG are congruent. Post a comment or solution.
 

See Also:

Proposed Problem 414.
Triangle, Angles, Altitude, Median, Congruence.

Proposed Problem 412.
Triangle, Angles, Congruence.

Proposed Problem 411.
Triangle, Median, Angles.

Proposed Problem 410.
Two Regular Pentagons, Angle.
Puzzle: 22 piece polygons.