 |
|
Problem 292: Triangle, Parallel, Congruence, Similarity
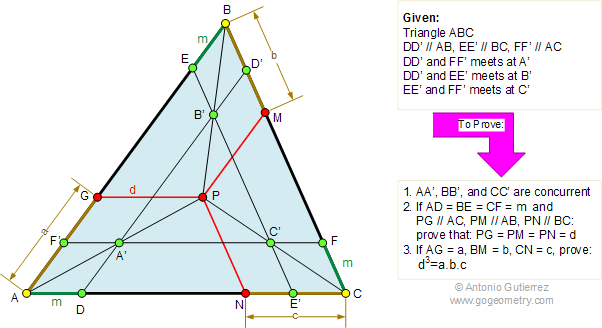
Level: High School, College, SAT Prep. The figure shows a triangle ABC, DD', EE', and FF'
are parallel to AB, BC, and AC, respectively. DD', EE', and FF'
intersect at A', B', and C', respectively. (1) Prove that AA', BB', and
CC' are concurrent at P. (2) If AD = BE = CF = m and PG, PM and PN are parallel to AC, AB,
and BC, respectively, prove that PG = PM = PN = d. (3) If AG = a, PM =
b, and CN = c, prove that
Geometry problem solving
Geometry problem solving is one of the most challenging skills for students to learn. When a problem requires auxiliary construction, the difficulty of the problem increases drastically, perhaps because deciding which construction to make is an ill-structured problem. By “construction,” we mean adding geometric figures (points, lines, planes) to a problem figure that wasn’t mentioned as "given."
|
Recent Additions
 |
