|
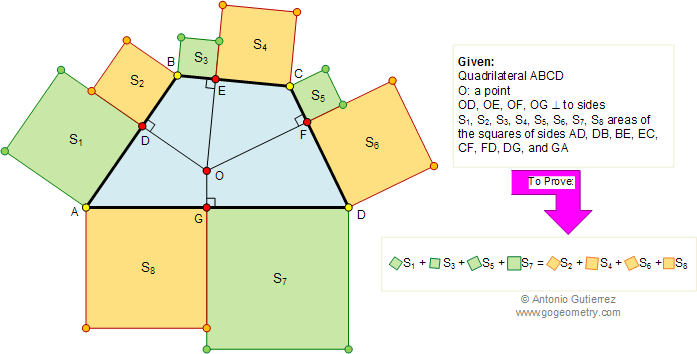
Problem 280: Quadrilateral, Perpendiculars, Area of Squares
In the figure below, from a point O inside or outside of a quadrilateral ABCD, perpendiculars are drawn to the sides meeting AB, BC, CD, AD at points D, E, F, and G, respectively. If S1, S2, S3, S4, S5, S6, S7, and S8 are the areas of the squares of sides AD, DB, BE, EC, CF, FD, DG, and GA, respectively, prove that S1 +S3 + S5 + S7 = S2 + S4 + S6 + S8 .
|
Recent Additions
|