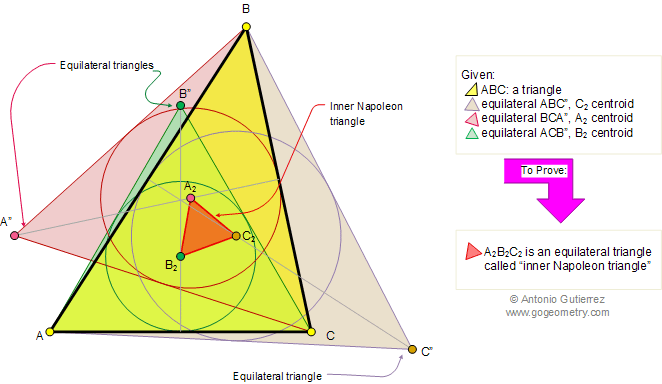
Problem 247. Napoleon's Theorem II. Internal Equilateral triangles. Inner triangle

In the figure, equilateral triangles ABC", BCA", and ACB" are constructed internally on the sides of a triangle ABC. Prove that the centers A₂, B₂, and C₂ of those equilateral triangles form an equilateral triangle, called the inner Napoleon triangle.
View or post a solution.

See also:
Problem 1205: Triangle, Centroid, Outer and Inner Napoleon Equilateral Triangles.
Problem 246: Napoleon's Theorem I. External Equilateral triangles. Outer triangle
Problem 248: Napoleon's Theorem III. Area Inner and Outer Napoleon triangles
iPad Apps: Apollonius: Napoleon's Theorem. External Equilateral Triangles