|
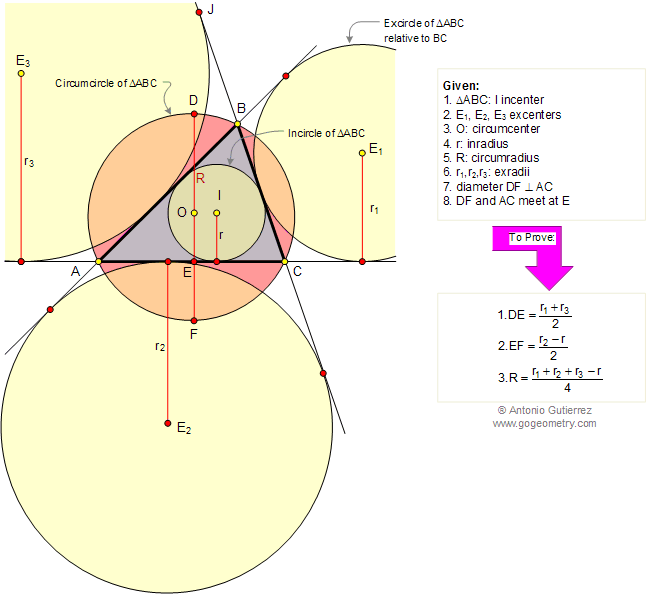
In the figure below, ABC is a triangle
inscribed in a circle of center O (circumcenter), I is the
incenter and
E1, E2, E3 are the excenters relatives to the sides BC,
AC, and AB respectively. Diameter DF of center O is
perpendicular to AC at point E. If R, r, r1, r2, r3 are the
circumradius, inradius and exradii respectively, (1) prove that
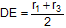 ,
(2) prove that ,
(2) prove that
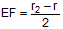 , and (3) prove that , and (3) prove that
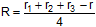 . .
|