|
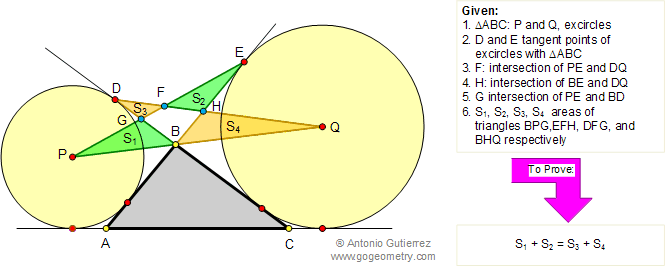
In the figure below, given a triangle
ABC, construct the excircles with
excenters P and Q. Let be D and E the tangent
points of triangle ABC with its excircles. PE and DQ meet at F,
BE and DQ meet at H, PE and BD meet at G. If S1, S2, S3,
and S4 are the areas of the triangles BPG, EFH, DFG, and
BHQ
respectively, prove that S1 + S2 = S3
+ S4.
View or post a solution.
 |