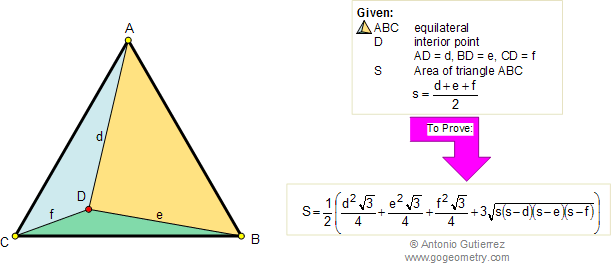
Geometry Problem 103. Equilateral Triangle Area, Interior Point, Heron.
Level: High School, College, SAT Prep.

In the figure below, given an equilateral triangle ABC, D is an interior point. If AD = d, BD = e, CD = f, and , prove that the area S of triangle ABC is:
Post a comment.
 

 

FACTS AND HINTS:

Geometry problem solving is one of the most challenging skills for students to learn. When a problem requires auxiliary construction, the difficulty of the problem increases drastically, perhaps because deciding which construction to make is an ill-structured problem. By “construction,” we mean adding geometric figures (points, lines, planes) to a problem figure that wasn’t mentioned as "given."

---

 USE

• Congruence of Triangles SAS

• Congruence of triangles SSS

• Heron's formula of area of a triangle

• Formula of the area of an equilateral triangle: , where s is any side.