Geometry Problems, Online Education

Problem 92. Similar Triangles, Circumcircles, Circumradii, Parallel. High School, College

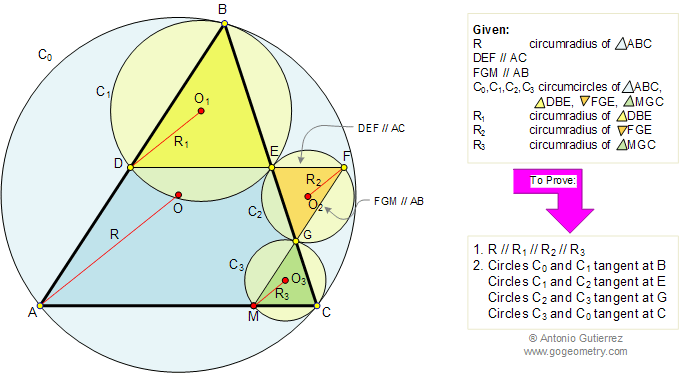
In the figure below, given a triangle ABC, circumcircle C0, circumradius R, line DEF parallel to AC and line FGM parallel to AB. C1, C2, and C3, and R1, R2, and R3 are the circumcircles and circumradii of triangles DBE, FGE, and MGC respectively, prove that: R // R1 // R2 // R3, and circles C0 and C1 are tangent at B, circles C1 and C2 are tangent at E, circles C2 and C3 are tangent at G, and circles C3 and C0 are tangent at C. View or post a solution.
 

Similar triangles, parallel, tangent circles. Elearning


 


FACTS AND HINTS:

1. SIMILAR TRIANGLES:
Proposition: Corresponding angles of similar triangles are congruent.

2. PROVING THAT LINES ARE PARALLEL:
Proposition: Two lines are parallel if a pair of corresponding angles are congruent.
Proposition: Two lines are parallel if a pair of alternate interior angles are congruent.

3. CIRCLES TANGENT:
Proposition: In the figure above, circles C0 and C1 are tangent internally if the line of center OO1 extended passes through B.
Proposition: In the figure above, circles C1 and C2 are tangent externally if the line of center O1O2 passes through G.

Home | Geometry | Search | Problems | Similarity | Circumcircle | All Problems | 91-100 | Email | View or post a solution | by Antonio Gutierrez