|
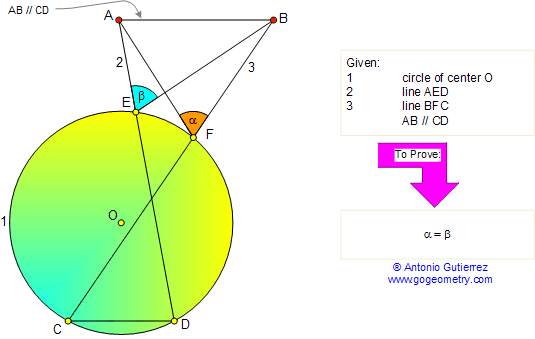
Given a circle (1), the lines AED (2)
and BFC (3). If AB is parallel to CD, prove that the angles AFB
and AEB are equal.
View or post a solution.
|
HINTS:
PARALLEL LINES
Proposition. If two lines
are parallel, each pair of alternate interior angles are
congruent. Also converse.
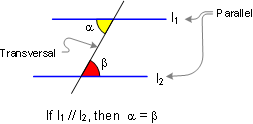
ANGLES IN A CIRCLE
Proposition. An inscribed angle is
measured by one-half its intercepted arc.

CYCLIC QUADRILATERAL is a quadrilateral whose
vertices all lie on a single circle.
Proposition 1.
Opposite angles of a cyclic (inscribed) quadrilateral are
supplementary. Also converse.

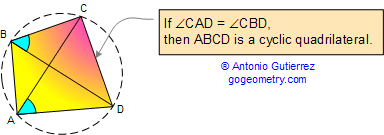
Proposition 2. A quadrilateral is cyclic if one side
subtends congruent angles at the two opposite vertices. Also
converse.
See also:
Problem 71
|