Geometry Problems, Online Education

Problem 75. Three Intersecting Circles, Cyclic Quadrilateral, Angles. Level: High School, SAT Prep, College

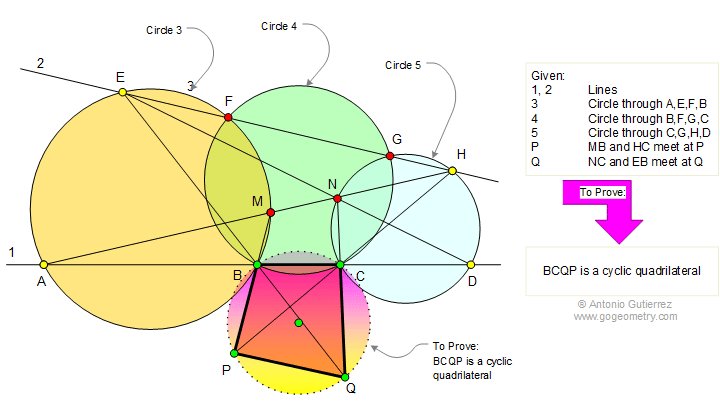
Given lines 1 and 2, circle 3 passes through the points A, E, F, B, circle 4 passes through the points B, F, G, C, and circle 5 passes through the points C, G, H, D. Line AH and circle 3 meet at M, Line DE and circle 5 meet at N. Lines MB and HC meet at a point P and lines NC and EB meet at a point Q. Prove that BCQP is a cyclic quadrilateral. View or post a solution.
 

Problem 75: Circles, Cyclic Quarilateral. Elearning
 

 

 

HINTS:

DEFINITION. A cyclic quadrilateral is a quadrilateral whose vertices all lie on a single circle.

PROPOSITION 1. Opposite angles of a cyclic (inscribed) quadrilateral are supplementary. Also converse.

PROPOSITION 2. A quadrilateral is cyclic if one side subtends congruent angles at the two opposite vertices. Also converse.

 
Home | Problems | 71-80 | Email | By Antonio Gutierrez