Geometry Problem 50 with Solution: Triangle with Equilateral triangles, (17) Conclusions

< PREVIOUS PROBLEM  |  NEXT PROBLEM >

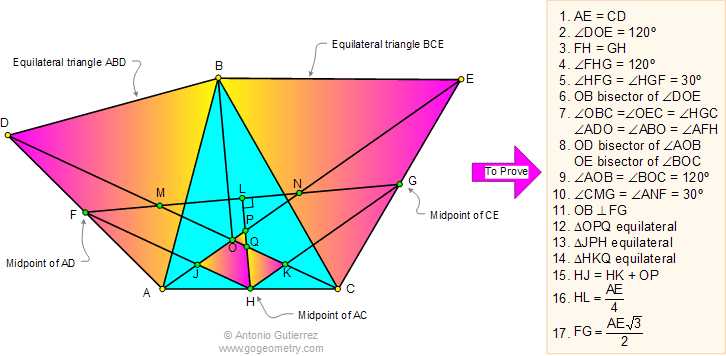
In the figure below, equilateral triangles ABD and BCE are drawn on the sides of a triangle ABC. F, G, and H are the midpoints of AD, CE, and AC respectively. HL and FG are perpendicular. Lines FH, CD, HL,  and FG are cut by line AE at J, O, P, and N respectively. Lines GH, HL, and FG are cut by line CD at K, Q, and M respectively. Prove the following:

1. AE = CD

2. The measure of angle DOE is 120�

3. FH = GH

4. The measure of angle FHG is 120�

5. m�HFG = m�HGF = 30�

6. OB is the bisector of �DOE

7. m�OBC = m�OEC = m�HGC
   m�ADO = m�ABO = m�AFH

8. OD is the bisector of �AOB
   OE is the bisector of �BOC

9. m�AOB = m�BOC = 120�

10. m�CMG = m�ANF = 30�

11. OB and FG are perpendicular

12. Triangle OPQ is equilateral

13. Triangle JPH is equilateral

14. Triangle HKQ is equilateral

15. HJ = HK + OP

16. 

17. 

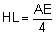
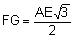
See solution below

Hints: See Geometry Help