Geometry Problem 39 with Solution: Triangle, Angle Bisector, Incircle, Cyclic Quadrilaterals. (15) Conclusions

< PREVIOUS PROBLEM  |  NEXT PROBLEM >

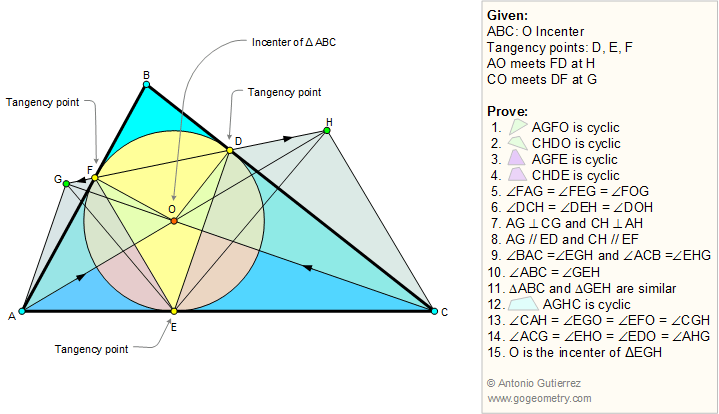
A circle of center O inscribed in a triangle ABC is tangent to sides BC, AC, and AB at points D, E, and F, respectively. Lines AO and FD meet at H, and lines CO and DF meet at G. Prove the following:

1. AGFO is a cyclic quadrilateral

2. CHDO is a cyclic quadrilateral

3. AGFE  is a cyclic quadrilateral

4. CHDE  is a cyclic quadrilateral

5. Angles FAG, FEG and FOG are congruent

6. Angles DCH, DEH and DOH are congruent

7. AG is perpendicular to CG and CH is perpendicular to AH

8. AG is parallel to ED and CH is parallel  to EF

9. Angles BAC and EGH are congruent and angles ACB and EHG are congruent

10. Angles ABC and GEH are congruent

11. Triangles ABC and GEH are similar

12. AGHC is a cyclic quadrilateral

13. Angles CAH, EGO, EFO, and CGH are congruent

14. Angles ACG, EHO, EDO, and AHG are congruent

15. O is the incenter of triangle EGH

.

See solution below

See also:
Help of problem 39
Art of problem 39
Sketch of problem 39

Home | Geometry | Problems | Open Problems | 10 Problems | Art | 31-40 | Circle Tangent Line | Right triangle, Altitude and Incircle | Email | by Antonio Gutierrez
Last updated: Sep 19, 2014

Post or view a solution