Sangaku
Problem (An Old Japanese Theorem). Level: High School, SAT
Prep, College
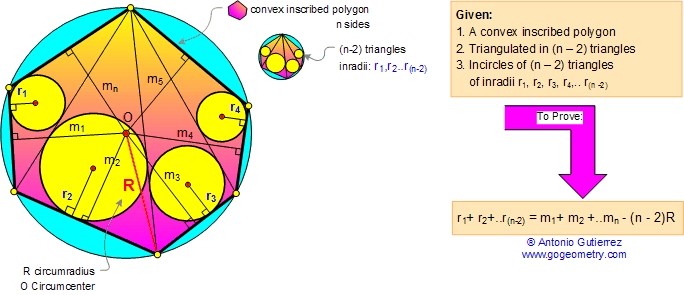
Let a convex inscribed polygon be
triangulated in any manner, and draw the incircle to each
triangle so constructed. Then the sum of the inradii is a
constant independent of the triangulation chosen. Hints:
Carnot's Theorem.
