|
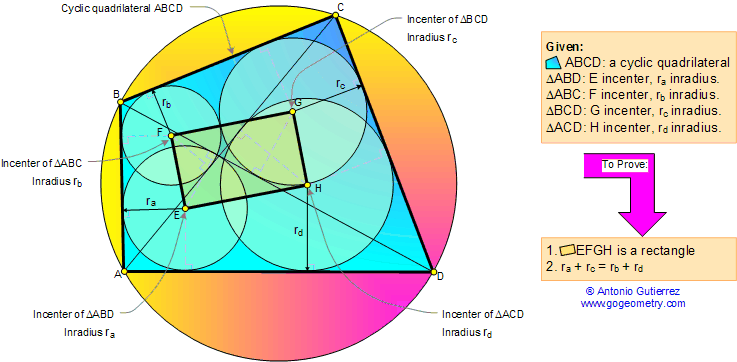
The figure shows a
cyclic
quadrilateral ABCD. E, F, G, and H are the
incenters and ra,
rb, rc, and rd are the
inradii
of the triangles ABD, ABC, BCD and ACD respectively. Prove that
EFGH is a rectangle and ra + rc = rb
+ rd. See the
proof.
References: Fukagawa Hidetoshi, Tony Rothman, "Sacred
Mathematics: Japanese Temple Geometry" (Princenton
University Press, 2008).
I have used
Geometry Expressions to visualize these geometric forms and
check out a variety of conjectures. Geometry Expressions is the
world's first Interactive Symbolic Geometry System. This means:
Geometric figures can be defined by either Symbolic Constraints
or numeric locations.
You can
download Geometry Expressions
2 Free Trial. It is a fully
featured 30 day evaluation copy of the software. All
constraints, constructions and measurements are available for
you to use.
Home |
Geometry |
Search |
Problems |
Sangaku
|
Email
|