|
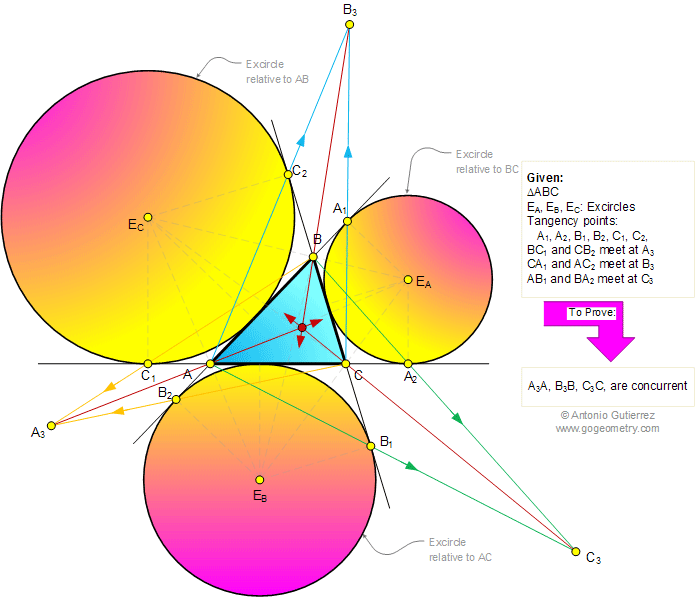
Problem 689: Triangle, Three Excircles, Tangency points, Tangent lines,
Concurrent Lines
The figure shows a triangle ABC with
the excircles EA, EB, and EC tangent to the
extension of sides at the points
A1, A2, B1, B2, C1,
and C2. Lines BC1 and CB2 meet at A3,
CA1 and AC2 meet at B3, AB1
and BA2 meet at C3. Prove that lines A3A,
B3B, and C3C are concurrent.
How to Solve It, Interactive Mind Map
George Pólya's 1945 book "How to Solve It, A new
aspect of Mathematical Method", is a book
describing methods of problem solving. It
suggests the following steps when solving a
mathematical problem: (1) First, you have to
understand the problem. (2) After understanding,
then make a plan. (3) Carry out the plan. (4)
Look back on your work. How could it be better? Mind Map Help. To see a note: Hover over a yellow note button. To Fold/Unfold: click a branch. To Pan: click and drag the map canvas.  |
Recent Additions
|