|
In the figure below, given a
triangle ABC, AD, BE, and CF are concurrent cevians at G. Prove
that:

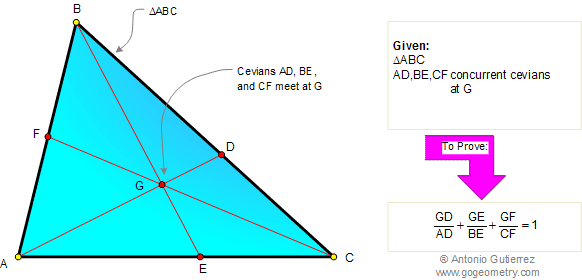 |
FACTS AND HINTS:
Geometry theorem proving is one of the most challenging skills for students to learn. When a proof requires
auxiliary construction, the difficulty of the problem increases
drastically, perhaps because deciding which construction to make is an ill-structured problem.
By “construction,” we mean adding geometric figures (points, lines, planes) to a problem figure that wasn’t mentioned as
"given."
1. CEVIAN:
A cevian is a line segment which joins a vertex of a triangle with a point on the opposite side (or its extension).
2. AREA OF A TRIANGLE:
Proposition:
The area of a triangle equals
one-half the product of the length of a side and the length of
the altitude to that side.
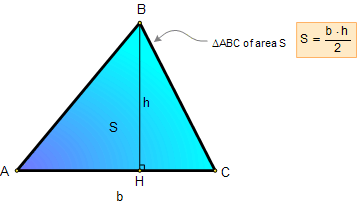
|