Euclid's Elements - Table of Content
|
|
 |
Euclid's Elements is a mathematical and geometric treatise consisting of
13 books written by the Greek mathematician Euclid in Alexandria circa
300 BC. It comprises a collection of definitions, postulates (axioms),
propositions (theorems and constructions), and proofs.
|
|
 |
Euclid's Elements
Book I, 23 Definitions.
One-page visual illustration. |
|
 |
Euclid's Elements Book I, Proposition 1: On a given finite line to
construct an equilateral triangle |
|
 |
Euclid's Elements Book I, Proposition 2: To place at a given point (as
an extremity) a straight line equal to a given straight line |
|
 |
Euclid's Elements Book I, Proposition 3: Given two unequal straight
lines, to cut off from the greater a straight line equal to the less |
|
 |
Euclid's Elements Book I, Proposition 4: (Side-Angle-Side SAS) |
|
 |
Euclid's Elements Book I, Proposition 5: (Pons Asinorum) Isosceles
triangles |
|
 |
Euclid's Elements Book I, Proposition 6: Converse of I.5
"Proof by contradiction," also called reductio ad absurdum. |
|
 |
Euclid's Elements Book I, Proposition 7
Given two straight lines constructed on a straight line (from its
extremities) and meeting in a point,... |
|
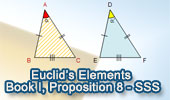 |
Euclid's Elements Book I, Proposition 8: (Side-Side-Side SSS Congruence) |
|
 |
Book I, Proposition 9: Bisect a given angle
|
|
 |
Book I,
Proposition 47th: Pythagoras
Pythagorean Theorem.
|
|
 |
The significance of the Pythagorean theorem by Jacob
Bronowski.
Pythagorean Theorem, 47th Proposition of Euclid's Book I. |
|
 |
Euclid's Elements Book I Word Cloud.
|
|
 |
Euclid's Elements Book II, Proposition 12: Law of Cosines.
|
|
 |
Euclid's Elements Book V Word Cloud.
A treatise on proportions of magnitudes. Proposition 25 has as a special case
the inequality of arithmetic and geometric means. |
|
 |
Euclid's Elements Book IV Word Cloud.
Constructs the incircle and circumcircle of a triangle, and constructs regular
polygons with 4, 5, 6, and 15 sides |
|
 |
Euclid's Elements Book III Word Cloud.
|
|
 |
Euclid's Elements Book II Word Cloud.
|
|
 |
Euclid's Elements Book II, Proposition 13: Law of Cosines.
|
|
 |
Euclid's Elements Book VI, Proposition 3: Angle Bisector Theorem
|
|
 |
Euclid's
Elements, Book X, Lemma for Proposition 33 One page visual illustration. |
|
 |
Euclid's
Elements, Book XIII, Proposition 10 One page visual illustration. |
|
 |
MindMap of
Euclid's Elements. A mindmap is an excellent learning tool for
visual communication, organization, content sequencing, and navigation
on Internet. |
|
 |
MindMap of Euclid's Elements Book I
|
|
 |
The School of Athens
Euclid and Pythagoras together!
Video |
|
 |
Twin
Prime Conjecture. is a famous unsolved problem in number theory
discovered by Euclid.
|
|
 |
Euclid's Quotes. |