|
Classical Theorems - Page 2
|
|
 |
|
|
 |
Euler's
Polyhedron Theorem |
|
 |
Pascal's Mystic Hexagram Theorem Proof |
|
 |
Pappus Theorem. Dynamic Geometry.
Step-by-Step construction, Manipulation, and animation. |
|
 |
Apollonius' Tangency Problem for Three Circles
Illustration with animation and sound.
|
|
 |
Feuerbach Point Theorems
|
|
 |
Feuerbach Points and Nine-Point Circle with interactive
animation, manipulation, and step-by-step construction. |
|
 |
Angle between two
Simson Lines. Proof with animation.
|
|
 |
Simson Line. A proof
of Simson line with animation. |
|
 |
Interactive Simson
Line. Dynamic Geometry.
Step-by-Step construction, Manipulation, and animation. |
|
 |
Lune of Hippocrates Index |
|
 |
Lune of Hippocrates 4: Circle Areas and Right |
|
 |
Hippocrates and Squaring the Circle
|
|
 |
Stewart Theorem Triangle and a cevian.
|
|
 |
Viviani's Theorem, Problem 221. Viviani's theorem, Equilateral triangle,
Interior point, Distances. |
|
 |
Eyeball Theorem:
Animated Angle to Geometry Study. |
|
 |
Blanchet Theorem
|
|
 |
Sawayama -Thebault's
theorem |
|
 |
Routh's Theorem - Index
Triangle, Cevians, Area, Ratio.
|
|
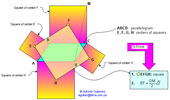 |
Parallelogram with Squares theorem Thébault's Theorem.
|
|

|
Johnson's Theorem,
Intersecting circles.
HTML5 Animation
Adobe Flash Animation |
|
 |
Varignon and Wittenbauer theorems. Quadrilateral: midpoints and
trisection points of the edges.
|
|
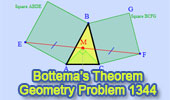 |
Bottema's Theorem:
Triangle and Squares with Interactive Geometry Software
Step-by-Step construction, Manipulation, and animation. |
|
 |
Morley's Theorem.
Introduction with animation. Triangle + Trisectors = Equilateral
triangle.
|
|
 |
Monge &
d'Alembert Three Circles Theorem II with Dynamic Geometry
You can alter the geometric construction dynamically in order to test
and prove (or disproved) conjectures and gain mathematical insight that
is less readily available with static drawings by hand. Requires
Java Plug-in 1.3 or higher. Please be patient while the applet loads
on your computer. If you are using a dial-up connection, it may take a
few minutes but is well worth the wait. Cabri, GSP, Cinderella,
C.a.R. |
|
 |
Monge &
d'Alembert Three Circles Theorem I with Dynamic Geometry
You can alter the geometric construction dynamically in order to test
and prove (or disproved) conjectures and gain mathematical insight that
is less readily available with static drawings by hand. Requires
Java Plug-in 1.3 or higher. Please be patient while the applet loads
on your computer. If you are using a dial-up connection, it may take a
few minutes but is well worth the wait. Cabri, GSP, Cinderella,
C.a.R. |
|
Go to Page:
Previous |
1 |
2 |
3 |
4 |
5 |
Next
|