 |

|

Geometry Problem 457: Triangle, First Brocard Point, Congruent angles, Circle, Circumradius, Common Chord.
|
|
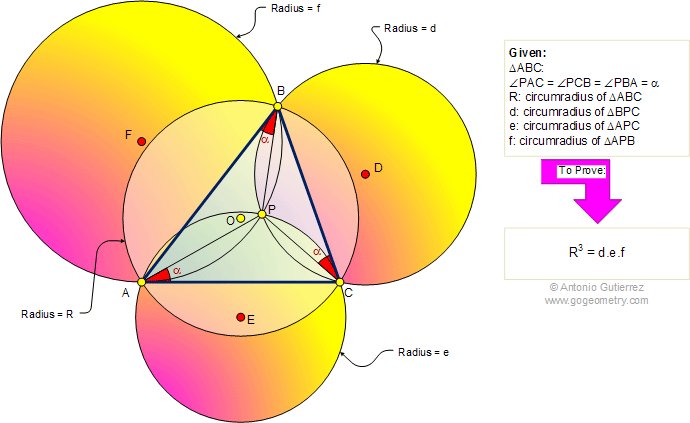
The figure shows a triangle ABC with
circumradius R. The angles PAC, PCB, and PBA are congruent. If d, e, and
f are the circumradii of triangles BPC, APC, and APB, respectively,
prove that R3 = d.e.f.
Point P is called the first Brocard point of the triangle ABC. The
circumradius is the radius of the circumcircle. The circumcircle of a
triangle is a circle which passes through all the vertices of the
triangle.
|
|
|
|
More Problems:
|
|
|
 |
Proposed Problem 458.
Square, Semicircle, Circular Sector, Internal Common Tangent,
Measurement. |
|
|
 |
Proposed Problem 456.
Three tangent circles, Center, Chord, Secant, Collinear. |
|
|
 |
Proposed Problem 455.
Rhombus, Inscribed Circle, Angle, Chord, 45 Degrees. |
|
|

 |
|
|
|
|
|
|
 |
 |
