Let A, B, C, D, E, F be points on a circle and makes a hexagon out of them in an arbitrary order. Then the three points L, M, N at which pairs of opposite sides meet, lie on a straight line. This line is called the Pascal line of the hexagon ABCDEF.
 
 

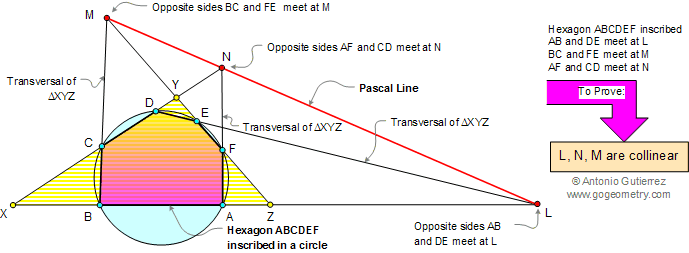
Proof:

1. Applying Menelaus’ Theorem respectively to transversal BCM, AFN, and DEL of triangle XYZ:

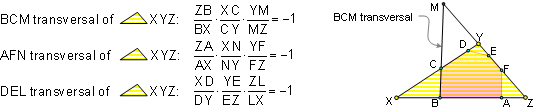
2. Multiplying the three identities, we get:

3. Using the intersecting secant theorem, we get:

4. By substituting (3) into (2), we get:

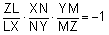
Thus, by the converse of Menelaus' Theorem, points M, N, and L lie on a transversal of triangle XYZ, therefore must be collinear. Q.E.D.
 

Blaise Pascal (1623-1662) French mathematician, philosopher and inventor, discovered his famous theorem at the age of 16, in 1640, and produced a treatise on conic sections entitled Essai pour les coniques.

See also:
Geometric art of the Pascal's theorem